
Complete Sum-Free Sets (Blog)
Over the course of my spring semester of my first year at Gettysburg College, I begun math research under the supervision of Professor Béla Bajnok using his book "Additive Combinatorics: A Menu of Research Problems" as my...

Complete Sum-Free Sets (Paper)
Click to read the PDF (Posted May 11 2021) (Be warned: This contains unrefined first-year undergraduate mathematical writing.)
Signed Zero-Sum-Free Sets and Signed Sum-Free Sets (Blog)
This summer, one topic that I have tackled is the concept of signed zero-sum-free sets. Currently...
Three Sum Free Problems
This is a collection of similar results attained during my time conducting research during the summer of 2021. I do not feel that any of theseresults warranted a separate paper as they stand. However...
Quotient Rings
A concept nearly omnipresent in mathematics is the simultaneous tool and idea of modular arithmetic. Modular arithmetic is almost always done over the integers, and in most scenarios...
A Special Case Of The Restricted 3-Critical Number
Conisder the following question: If $G$ is a finite abelian group, and $h$ is a positive integer, what is the smallest $m$ such that every $m$-subset of $G$, $A$, has the property that every element of $G$ is representable as the sum of exactly $h$ (not nessecarily distinct) elements of $A$? For those of you familiar with my previous blogs...
.png)
An Investigation and Documentation of Social Choice Functions
In 2016 Donald Trump won the American presidency despite receiving nearly three million fewer votes than the leading candidate, Hillary Clinton. With occurrences like this many Americans have called for election reform so that the results of our elections more accurately reflect the preferences of America’s population. In the modern world, the demand for fair and reliable...
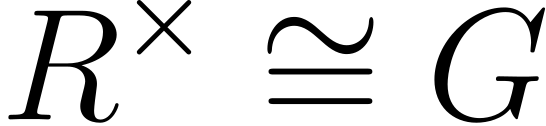
Fuchs' Problem for Linear Groups
Which groups can occur as the group of units in a ring? Such groups are called realizable. Though the realizable members of several classes of groups have been determined (e.g., cyclic, odd order, alternating, symmetric, finite simple, indecomposable abelian, and dihedral), the question remains open. The general linear groups are realizable by definition: they are the units in the corresponding matrix rings. In this paper, we study the realizability of two closely related linear groups... (To appear in Communications in Algebra)
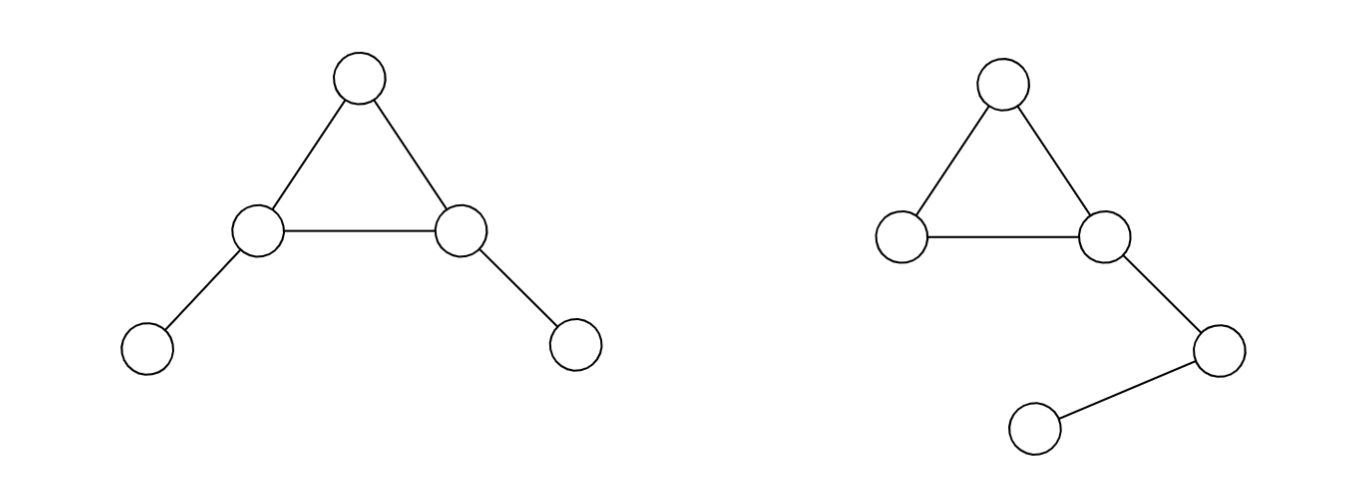
Inequalities and Implications Involving the Adjacency Spectrum of a Graph
In this paper, we will be diving into linear algebraic graph theory. Specifically, we will be exploring how the eigenvalues of a particular matrix representation of a graph impact its graph-theoretic properties. In Section 3 we will introduce the vocabulary needed to properly understand the subsequent sections. Section 4 will provide the linear algebraic background...
Dissociativity In Abelian Groups
Maximum Size Zero-Sum-Free Sets in Cyclic Groups
Minimum Size $h$-Fold restricted sumsets in $\mathbb{Z}_2^r$
Minimal Size $2$-fold Restricted Sumsets of $2p+1$-Subsets of $\mathbb{Z}_p^2$
Sets with a small number of signed sums
Variants of the Zero-Sum-Free Problem in Finite Abelian Groups
Research Interests
- Additive Combinatorics, specifically Zero-Sum-Free problems, subset sum problems, and other extremal problems concerning sumsets
- Commutative Algebra, Fuchs' Problem.
- Graph theory. Specifically: characterization of graphs with specific spectral properties
- Anything that you have the time to talk to me about!